Voici un extrait du livre II de l'Introduction arithmétique de Nicomaque de Gérase qui explique la manière dont on peut décomposer un p-gone d’ordre n en un (p-1)-gone d’ordre n et un triangle d’ordre n-1 :
Prends donc deux triangles que tu combines entre eux, tu obtiendras un carré parfait et, par conséquent, en brisant un carré quelconque, tu pourras obtenir deux triangles à partir de ce carré. Et de même un triangle ajouté à toute figure carrée donnera un pentagone quelconque ; c’est ainsi qu’un carré de 4 points ajouté à un triangle de 1 [point] donne un pentagone de 5 [points] et que le triangle suivant, évidemment de 3, ajouté de proche en proche à [un carré de] 9, donne un pentagone de 12 tandis que le [triangle] suivant, de 6, ajouté au [carré] suivant de 16, atteindra 22, de même que celui de 10 ajouté à celui de 25 donnera 35, et ainsi de suite sans cesse [1].
Le tableau suivant, présenté par Nicomaque, permet de comprendre toutes les décompositions possibles à la manière d'un triangle de Pascal:
|
|
Longueur et largeur |
|
|||||||||
|
Triangles |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
Profondeur |
|
Carrés |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
|
Pentagones |
1 |
5 |
12 |
22 |
35 |
51 |
70 |
92 |
117 |
145 |
|
|
Hexagones |
1 |
6 |
15 |
28 |
45 |
66 |
91 |
120 |
153 |
190 |
|
|
Heptagones |
1 |
7 |
18 |
34 |
55 |
81 |
112 |
148 |
189 |
235 |
|
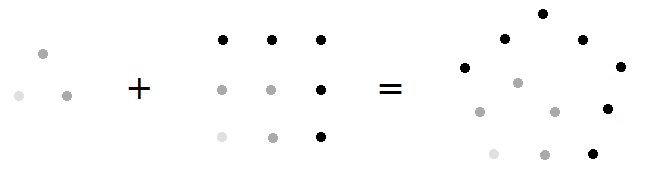
Abonnez-vous à notre infolettre!
Pour ne rien rater de l'actualité scientifique et tout savoir sur nos efforts pour lutter contre les fausses nouvelles et la désinformation!
[1]. Traduction par Antoine Houlou-Garcia et Alain Houlou, in Mathematikos, Les Belles Lettres, 2019, pp. 98-99.













